S&OP e Famílias de Produtos

Veja neste artigo porque é melhor utilizar Famílias de Produtos na projeção de vendas do S&OP – exemplo utilizando Python

Introdução

Um dos componentes do ‘Sales and Operations Planning’ (S&OP) é a projeção de vendas para os próximos 12 (ou 24) meses. E a recomendação é que seja feita por Família de produtos. O motivo é devido aos desvios (em relação à média) serem muito menores que os de cada produto individualmente.

Vamos entender melhor essa recomendação com um exemplo utilizando Python, uma linguagem de programação popular, conhecida pela sua simplicidade e versatilidade. Amplamente utilizada em desenvolvimento de software, automação, análise de dados e aprendizado de máquina, Python oferece uma variedade de bibliotecas poderosas para facilitar o desenvolvimento de aplicativos eficientes. É especialmente valorizada na ciência de dados devido às suas robustas bibliotecas como NumPy, pandas, matplotlib e scikit-learn.

Bibliotecas utilizadas:

import pandas as pd
import numpy as np
import plotly.graph_objects as go
import plotly.subplots as sp

A base de dados que vamos utilizar é um relatório de movimentação de estoque. Com Data da movimentação, Tipo de Movimento, Código de Produto, Família de Produto, e valores de entrada e saída (Quantidade, Valor em R$, Peso e Volume).

Base de dados:

f_mov2

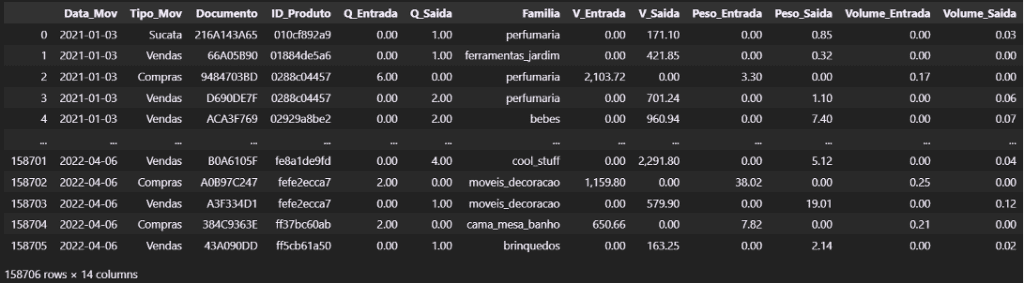
Vamos gerar um Pareto por Família de Produto para escolhermos uma para o estudo.

pareto_familias = f_mov2.groupby([
    'Familia'
]).agg(
    V_Saida      = ('V_Saida',      'sum'),
    Freq_Saida   = ('V_Saida',      'count'),
    Peso_Saida   = ('Peso_Saida',   'sum'),
    Volume_Saida = ('Volume_Saida', 'sum'),
    Q_Prod_Saida = ('ID_Produto',   'nunique')
).sort_values(
    by = 'V_Saida', ascending = False
).reset_index()

pareto_familias

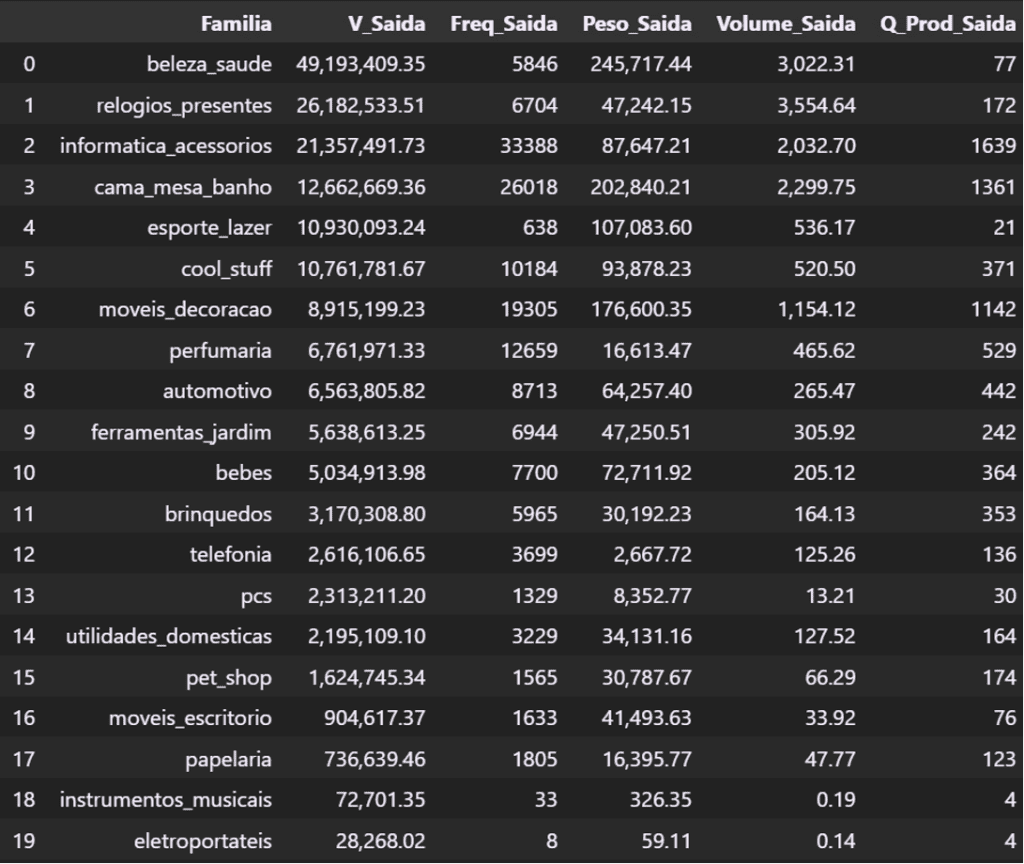
Escolhemos a família ‘informatica_acessorios’, que possui uma grande quantidade de produtos, é a terceira em Valor e a primeira em frequência.

Vamos precisar também de um Pareto por Produto para utilizarmos nas visualizações.

pareto_produto = f_mov2.loc[
    f_mov2['Familia'] == 'informatica_acessorios'
].groupby([
    'ID_Produto', 'Familia'
]).agg(
    V_Saida      = ('V_Saida',      'sum'),
    Freq_Saida   = ('V_Saida',      'count'),
    Peso_Saida   = ('Peso_Saida',   'sum'),
    Volume_Saida = ('Volume_Saida', 'sum')
).sort_values(
by = 'V_Saida', ascending = False
).reset_index()

pareto_produto

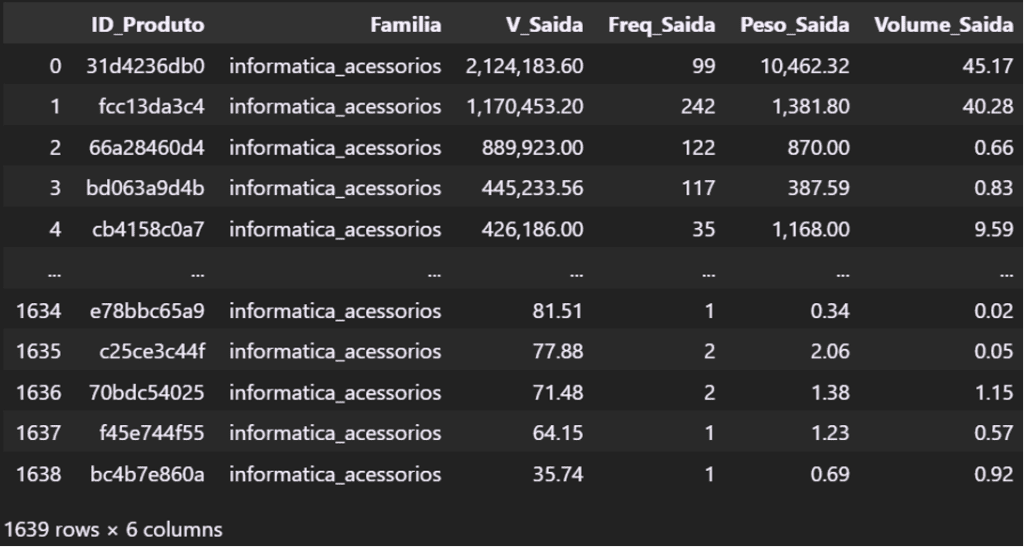
Com os dados carregados e tratados vamos criar uma função que gere um gráfico das Saídas diárias, com a média e o desvio padrão, e outro gráfico com um histograma das mesmas saídas diárias. Assim poderemos observar como o desvio se comporta com diferentes quantidades de produtos.

A função abaixo começa recebendo uma quantidade de produtos, que será utilizada para filtrar do primeiro produto até a quantidade informada da tabela de Pareto por Produto, e se nada for informado utilizará o total de produtos da família. Depois gera um resumo diário das Saídas por Vendas, calcula a média e o desvio padrão, gera um gráfico de colunas com as saídas diárias, em valor, e um histograma dos valores diários.

def familia_e_QTD_produtos( Q_Produtos_ = pareto_produto['ID_Produto'].nunique() ):
    familia = pareto_produto['Familia'][0]

    f_mov2_familia = f_mov2.loc[
        (f_mov2['Familia'] == familia) & (f_mov2['Tipo_Mov'] == 'Vendas')
    ]

    resumo_diario = f_mov2_familia.loc[
        (f_mov2_familia['ID_Produto'].isin(pareto_produto['ID_Produto'][0:Q_Produtos_])) &
        (f_mov2_familia['Tipo_Mov'] == 'Vendas') 
    ].groupby([
        'Data_Mov'
    ]).agg(
        V_Saida = ('V_Saida', 'sum')
    ).reset_index()

    media_saidas = np.mean(resumo_diario['V_Saida']).round(0)
    desvP_saidas = np.std(resumo_diario['V_Saida']).round(0)
    desvP_saidas_percent = ((desvP_saidas / media_saidas) * 100).round(1).astype(str) + '%'

    fig = sp.make_subplots( rows = 2, cols = 1 )

    fig.add_trace(
        go.Bar(
            x = resumo_diario['Data_Mov'],
            y = resumo_diario['V_Saida'],
            name = 'V_Saida_Diaria'
        ), 
        row = 1, col = 1
    ).update_traces(
        marker_line_width = 0,
    ).update_yaxes( gridwidth = 2.0 ).update_xaxes( showgrid = True, gridwidth = 2.0 )

    fig.add_hline(
        y = media_saidas, opacity = 0.7, line_color = 'darkblue', 
        annotation_text = 'media_saidas'
    )
    fig.add_hline( 
        y = media_saidas + desvP_saidas, opacity = 0.7, line_color = 'darkred', 
        annotation_text = '+ desvP_saidas' 
    )

    fig.add_trace(
        go.Histogram( 
            x = resumo_diario['V_Saida'],
            name = 'curva de Frequência'
        ),
        row = 2, col = 1
    ).update_traces(
        marker_line_width = 1.3
    )

    fig.update_layout(
        title = "" + familia + ", " + str(Q_Produtos_) + " Produtos" + "
" +
            "Valor saída média: " + str(int(media_saidas)) + ", " + 
            "Desvio padrão: " + str(int(desvP_saidas)) + " -> " + 
            desvP_saidas_percent,
        title_font = dict(family = 'consolas'),
        height = 800
    )

    return fig

Com tudo pronto vamos testar algumas quantidades de Produto e observar o resultado.

familia_e_QTD_produtos( 5 )

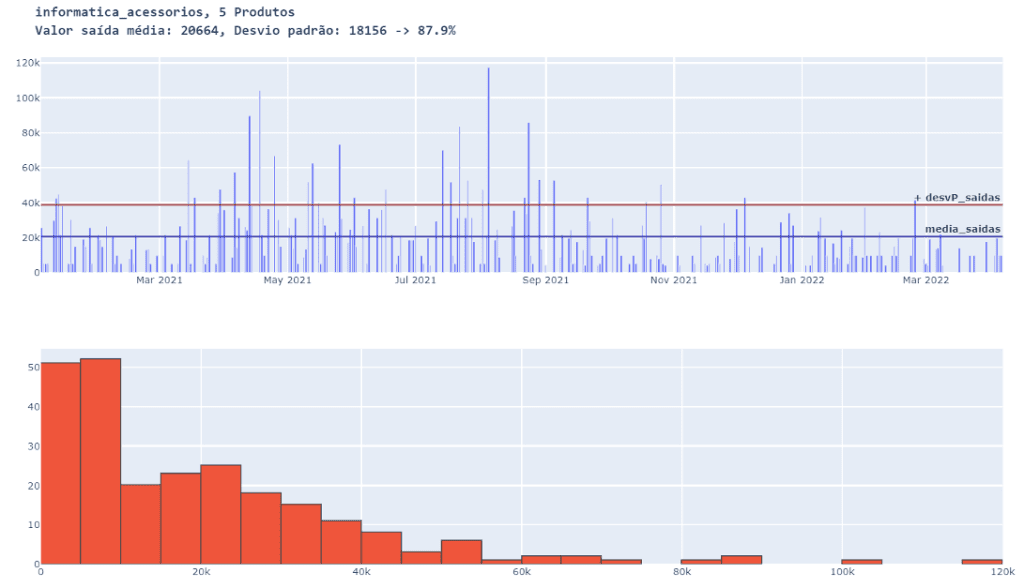
Com 5 produtos observamos que as saídas possuem um grande desvio padrão, ou seja, uma projeção de vendas se torna pouco assertiva.

Vamos testar com mais produtos e comparar.

familia_e_QTD_produtos( 50 )

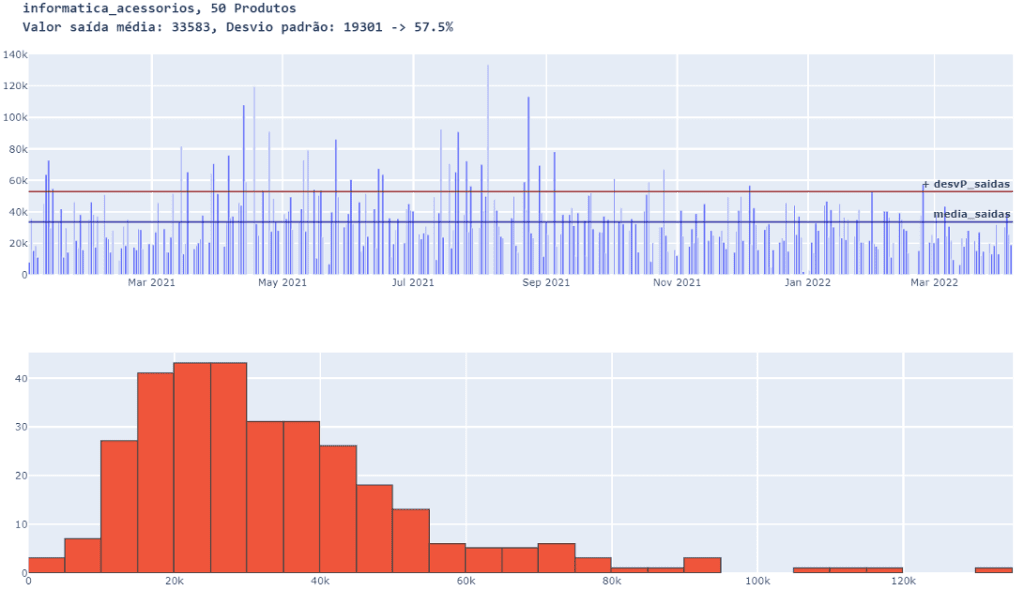
Com 50 produtos é notável a redução do desvio. Vamos adicionar mais produtos e observar se o desvio diminui ainda mais.

familia_e_QTD_produtos( 500 )

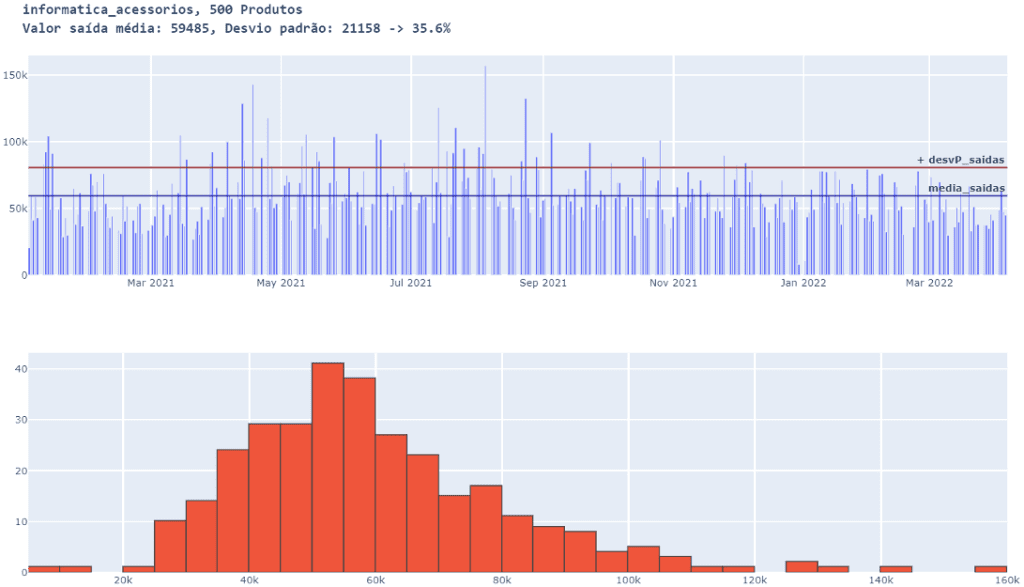
Com 500 produtos também é notável a redução do desvio em relação a 50. Menos desvio torna a projeção de vendas mais assertiva e confiável.

Para concluir vamos deixar todos os produtos da família e observar se há mais alguma redução significativa do desvio.

familia_e_QTD_produtos( )

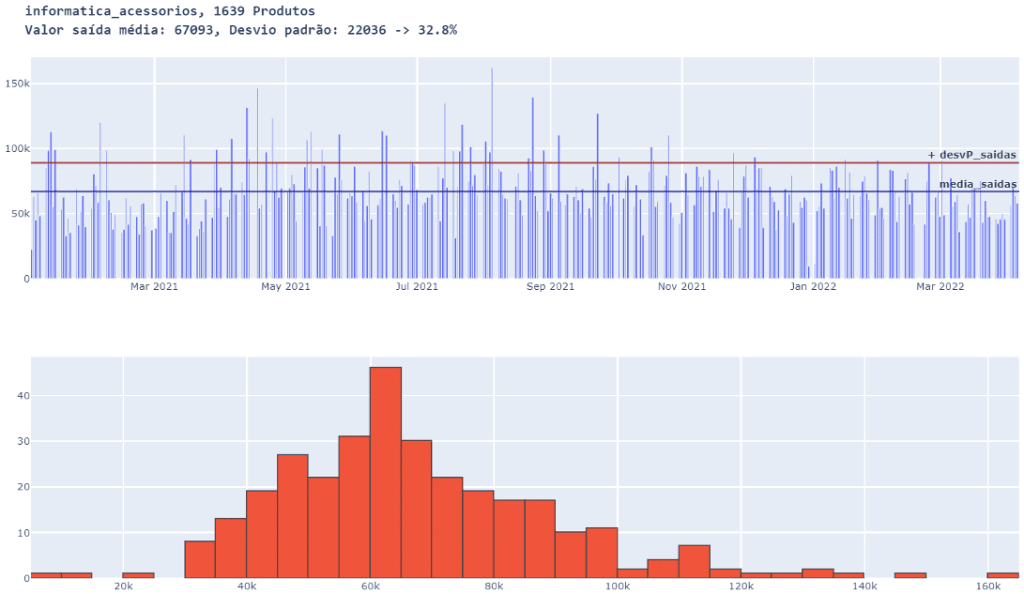
Ainda houve mais uma redução do desvio, mas não muito importante em relação a 500.

Muito obrigado por ler o artigo. Espero que tenham gostado!

Até o próximo!

Post Views: 71